As both chemists and flow artists know, all objects have symmetry. Types of symmetry can be defined as different “operations” where the object is moved in a certain way, but looks exactly the same before and after the movement takes place.
Symmetry Operations
E: The Identity Operation. The object is not moved. All objects have identity symmetry.
Cn: A rotation around an axis by 360/n°. The object is spun around an isolated axis.
σ: A mirror plane. An object is reflected across a plane.
i: Inversion. An object is inverted through a single point.
Sn: Improper rotation. An object is first rotated by 360/n°, then it is reflected across a plane perpendicular to that axis.
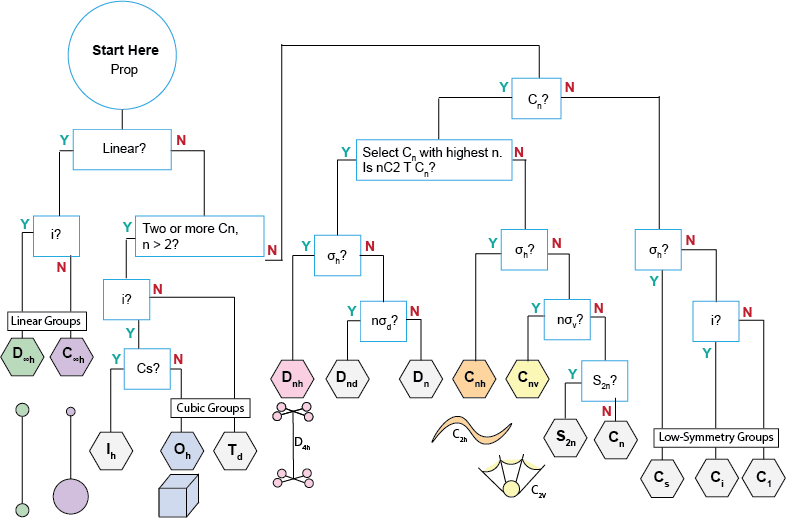

This flow chart can help us assign a point group to any prop–well, really, any object at all! Let’s try a fan. Starting from the top, we can see that a fan is not linear. It’s not very high symmetry: there is only one Cn axis, a C2 axis that runs along the center spine. If we tried to mirror the fan perpindicular to that axis, we will see there is no horizontal mirror plane. There are, however, two parallel mirror planes — one that goes through all the spines, and one that divides the spines in half. Therefore, the point group of a fan is C2V
So why does this matter? When we move props through space, they create a certain look or illusion. The exact same move, performed with different props, can look quite different. These groups allow us to relate props to each other in a formal and simple system, to gain a deeper understanding of each prop and their unique properties.